Wer hat sowas noch nicht erlebt. Der Alleinspieler in Mittelhand spielt Null Ouvert mit diesem Blatt:

Ich sitze in Hinterhand mit folgendem Blatt:

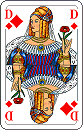
Erstmal kein gutes Blatt für einen Null Ouvert. Aber nach einer kurzen Analyse stellt man fest, dass der Alleinspieler in Kreuz zu bekommen ist. Vorhand spielt klein Kreuz, ich übernehme mit dem Ass. Dann Vorhand in Karo wieder an den Stich bringen und der spielt wieder Kreuz, das ich mit dem König übernehme. Über meinen Kreuz Buben muss dann der Alleinspieler drübergehen.

Zudem gibt es auch eine Chance in Herz, auch wenn diese Möglichkeit etwas schwieriger ist. Vorhand spielt klein Karo, ich übernehme mit dem König. Dann Herz Ass vorspielen und wieder ein kleines Karo, das Vorhand mit dem Ass übernimmt. Er spielt nochmals Karo und ich werde meinen Herz König los.

Am Ende gewinnt der Alleinspieler. Was war passiert?

Ich habe ein sehr schwaches Blatt für das Null-Gegenspiel. Ich habe gerade einmal eine Möglichkeit (Karo Ass), meinen Partner wieder ans Spiel zu bringen. Ist diese Möglichkeit nicht mehr gegeben und ich komme an den Stich, mache ich unweigerlich alle restlichen Stiche.

Das Problem an diesem Blatt ist, dass es trotz meines schwachen Gegenblattes möglich ist, den Spieler in zwei Farben zu bekommen. Allerdings müssen sich beide Gegenspieler in der Farbe einig sein. Und genau deshalb hat der Alleinspieler sein Spiel gewonnen. Der Spieler in Vorhand verfolgt die eine Strategie und ich die andere. Und schnell ist ein kleiner Fehler passiert und ich komme nicht mehr vom Stich.

Beispiel 1: Vorhand spielt Herz aus mit der Absicht, den Alleinspieler in dieser Farbe zu erwischen. Ich habe mich aber auf die Kreuz-Lösung eingestellt. Daher erkenne ich die Absicht nicht und versuche, Vorhand wieder ans Spiel zu bringen, damit er Kreuz spielen kann. Das misslingt aber, da ich dazu nur eine einzige Möglichkeit in Karo habe. Wechselt Vorhand nun tatsächlich auf Kreuz, mache ich die restlichen Stiche.

Beispiel 2: Vorhand spielt Herz aus. Sein Ziel ist es also, den Alleinspieler in Herz zu bekommen. Die richtige Strategie wäre nun, dass ich Karo ausspiele, Vorhand bleibt drunter, ich spiele erneut Karo und Vorhand nimmt das Ass. Dann kommt erneut Karo und ich werfe meinen Herz König ab. Statt das erste Karo laufen zu lassen, nimmt er aber gleich das Ass und spielt mich erneut in Karo ein. Ich kann ihn aber jetzt nicht mehr ans Spiel bringen und mache alle restlichen Stiche.

Sicher: Einer der Gegenspieler muss einen Fehler machen, damit der Alleinspieler sein Spiel verliert. Ich wollte mit dem Beispiel verdeutlichen, dass es gerade bei Nullspielen sehr häufig vorkommt, dass jeder Gegenspieler eine andere Strategie verfolgen. Und statt sich auf die Strategie des Partners einzustellen, wird stattdessen versucht, seine Strategie mit „Gewalt“ durchzubringen.

Wäre der Alleinspieler in dem Beispiel nur in einer einzigen Farbe schwach gewesen, dann hätte er das Spiel vermutlich nie gewonnen, denn beide Gegenspieler stellen sich sofort auf diese eine Farbe ein und es kann keine Missverständnisse geben. Das Missverständnis wie in Beispiel 1 beschrieben kann dann erst gar nicht vorkommen.

Viele Spieler – auch die mit längerer Spielerfahrung – haben große Probleme mit dem Gegenspiel beim Null. Grund genug, sich das Spiel einmal etwas näher anzuschauen.

Ich gewinne ein Nullspiel genau dann, wenn ich keinen einzigen Stich mache.

Bei jedem anderen Spiel im Skat ist mein Ziel das genaue Gegenteil: Ich versuche, möglichst viele Stiche zu machen um mein Spiel zu gewinnen. Augen spielen beim Null übrigens gar keine Rolle, ich verliere auch dann, wenn ich einen Stich mit 0 Augen mache.

Beim Nullspiel gibt es keinen Trumpf.

Buben sind ganz normale Karten und werden im Rang vor der Dame einsortiert. Auch das gibt es nur beim Nullspiel. Eine weitere Konsequenz: Es gibt keine Spitzen. Das Nullspiel hat daher feste Grundwerte: 23 für einen „normalen“ Null, 35 für einen Null Hand, 46 für einen Null Ouvert und 59 für einen Null Ouvert Hand. Ach ja: Auch der Null Ouvert ist eine Besonderheit, alle anderen Spiele kann man im Skat nämlich nur dann offen spielen, wenn man aus der Hand spielt. Den Null Ouvert darf man auch nach Skataufnahme spielen. Es gibt auch keine weiteren Gewinnstufen. Jedes Nullspiel endet auf eine dieser beiden Möglichkeiten: Der Alleinspieler gewinnt oder verliert. Schneider oder Schwarz gibt es nicht.

Die 10 ist eingereiht.

Sie wird nicht vor dem Ass, sondern nach der 9 einsortiert. Wer kennt das nicht: Ein Spieler sagt ein Nullspiel an und plötzlich sind die Gegenspieler erstmal damit beschäftigt, ihre Handkarten neu zu sortieren.

Das Nullspiel ist also ein völlig anderes Spiel als alle anderen Spiele im Skat. Quasi ein „Spiel im Spiel“.

Der erste Stich beim Nullspiel dauert auch gerne einmal etwas länger. Die Gegenspieler müssen sich erstmal auf das Spiel einstellen. Eine für Farb- und Grandspiele bereits vorbereitete Taktik wird beim Nullspiel kaum Anwendung finden. Also muss man seine Taktik komplett überdenken.

Zudem gibt es relativ wenige Nullspiele. In einer Serie (36 Spiele) sind es meist gerade einmal zwei oder drei. Serien ganz ohne Nullspiele sind keine Seltenheit. Das Nullspiel wird auch gerne mal als Ausweichspiel genommen, wenn man schlecht gefunden hat und kein teures Farbspiel verlieren möchte. In diesem Fall ist es meist nicht schwierig, das Spiel „umzumachen“.

Man hat also stets mehr Spielpraxis bei Farb- und Grandspielen als bei Nullspielen. Klar: Bei Skatprofis, die bereits viele tausende von Spielen gespielt haben spielt das irgendwann keine große Rolle mehr, sie können schnell umdenken und sofort von „normalem“ Spiel auf Null umstellen. Aber der Weg dorthin ist beim Nullspiel wegen seines geringen Vorkommens deutlich länger.

Noch ein Beispiel?

Mittelhand spielt Null Ouvert mit diesem Blatt:

Hinterhand hat dieses Blatt:

Der Alleinspieler verliert, allerdings erst im achten Stich. Die Auflösung gibt es übrigens hier.

Und ein Klassiker, diesmal mit allen drei Blättern.

Mittelhand (spielt Null Ouvert):

Vorhand:

Und Hinterhand:

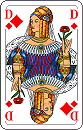
Auch dieser Null Ouvert ist „kaputtbar“. Die Auflösung gibt es hier.

Man stelle sich nun diese Spiele bei einem Turnier vor. Oder noch schlimmer, bei einem Online-Turnier, wo in der Regel noch schneller gespielt wird. Hand aufs Herz: wer hätte den Lösungsweg gefunden? Und leider wäre das noch nicht einmal genug, auch der Mitspieler muss den Lösungsweg finden und mitgehen.

Für den Alleinspieler ist das Spiel in der Regel relativ leicht zu spielen. Nur selten ergeben sich Situationen, in denen der Alleinspieler zu dem Ausgang des Spiels entscheidend beiträgt. Ein schönes Beispiel ist unser Spiel des Monats Mai 2011. Der Alleinspieler hat ein nicht allzu gutes Nullspiel, das aber auf Grund der Kartenverteilung absolut unverlierbar ist. Dennoch können die Gegenspieler den Alleinspieler in eine Situation bringen, in der er sich für eine von zwei Farben entscheiden muss. Und da er die Karten der Gegenspieler nicht kennt, kann er sich hier für die falsche Farbe entscheiden und das Spiel so doch für die Gegenspieler entscheiden.

So schwierig das Nullspiel für manche auch ist (und nicht selten wird am Tisch laut aufgestöhnt, wenn ein Spieler ein Nullspiel ansagt), so faszinierend ist das Spiel auch, wie die Beispiele deutlich machen. Sie zeigen nicht nur, wie schwierig ein Nullspiel sein kann, sie zeigen auch die Komplexität dieses besonderen Spiels.

Weiterlesen →